Все целые числа (кроме 0 и 1) имеют минимум два делителя: 1 и самого себя. Числа, не имеющие других делителей, называются простыми числами. Числа, имеющие другие делители, называются составными (или сложными) числами. Простых чисел – бесконечное множество. Ниже приведены простые числа, не превосходящие 200:

Всякое составное число может быть единственным образом представлено в виде произведения простых множителей. Например, 

48 = 2 · 2 · 2 · 2 · 3,    225 = 3 · 3 · 5 · 5,   1050 = 2 · 3 · 5 · 5 · 7 .

Расширение дроби. Сокращение дроби. Сравнение дробей.

Приведение к общему знаменателю. Сложение и вычитание дробей.

Умножение дробей. Деление дробей.

Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля. Это преобразование называется расширением дроби. Например,

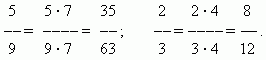Обыкновенная (простая) дробь. Числитель и знаменатель дроби.

Правильная и неправильная дробь. Смешанное число.

Неполное частное. Целая и дробная часть. Обратные дроби.

Часть единицы или несколько её частей называются обыкновенной или простой дробью. Количество равных частей, на которые делится единица, называется знаменателем, а количество взятых частей – числителем. Дробь записывается в виде:

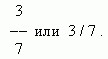
Алгебраическая дробь. Сокращение дробей.

Сложение и вычитание дробей. Умножение и деление дробей.

Алгебраическая дробь – это выражение вида  A / B,  где  A и B  могут быть числом, одночленом, многочленом. Как и в арифметике,  A называется числителем, B – знаменателем. Арифметическая дробь является частным случаем алгебраической.

В общем случае разложение многочленов на множители не всегда возможно. Но существует несколько случаев, когда это выполнимо.

 Линейный двучлен. Теорема Безу.

Линейный двучлен есть многочлен первой степени:   a x + b. Если разделить многочлен, содержащий букву  x , на линейный двучлен  x – b, где  b – некоторое число (положительное или отрицательное), то остаток будет только многочленом нулевой степени (см. параграф “Деление многочленов”), т.е. некоторым числом  N , которое можно определить, не находя частного. Более точно, это число равно значению многочлена, получаемому при  x = b. Это свойство вытекает из теоремы Безу:   многочлен  a₀ x^m + a₁ x^m-1 + a₂ x^m-2 + …+ a_m  делится на двучлен   x – b   с остатком  N = a₀ b^m + a₁ b^m-1 + a₂ b^m-2 + …+ b_m .

Логарифм. Основное логарифмическое тождество.

  Свойства логарифмов.  Десятичный логарифм. Натуральный логарифм.

Линейным  уравнением с одним неизвестным называется уравнение вида: