Логарифмы
Логарифм.
Основное логарифмическое тождество.
Свойства логарифмов.
Десятичный логарифм.
Натуральный логарифм.
Логарифмом
положительного числа N
по основанию
(
b >
0,
b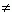 1
)
называется показатель
степени x
, в которую нужно
возвести
b,
чтобы
получить
N
. 1
)
называется показатель
степени x
, в которую нужно
возвести
b,
чтобы
получить
N
.
Обозначение логарифма:
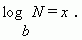
Эта запись равнозначна
следующей: bx
= N
.
П р и м е р ы :
log
81 = 4 , так как 34 = 81 ;
3
log
27 =
–
3 , так как ( 1/3 )
-3
= 33 = 27 .
1/3
Вышеприведенное определение логарифма можно записать в виде тождества:
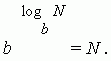
Основные свойства логарифмов.
1)
log b
= 1 ,
так как b
1
= b
.
b
2)
log
1 = 0 , так как b
0
= 1
.
b
3)
Логарифм произведения
равен сумме логарифмов сомножителей:
log ( ab ) = log a + log b .
4)
Логарифм частного равен разности
логарифмов делимого и делителя:
log ( a / b ) = log a –
log b .
5)
Логарифм степени равен произведению
показателя степени на логарифм её основания:
log ( b
k
) = k
·
log b .
Следствием этого свойства является
следующее: логарифм
корня
равен
логарифму подкоренного числа, делённому на степень корня:
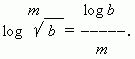
6)
Если в основании логарифма
находится степень, то величину,
обратную показателю
степени, можно вынести за знак логарифма:
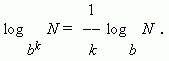
Два последних свойства можно объединить в одно:
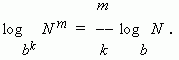
7)
Формула модуля перехода
( т.e.
перехода от одного основания
логарифма к другому основанию ):
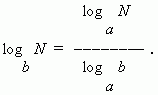
В
частном случае при
N
=
a
имеем:
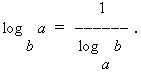
Десятичным
логарифмом
называется логарифм по основанию 10. Он обозначается
lg
, т.е. log
10
N
= lg
N
. Логарифмы чисел 10, 100, 1000, ...
pавны
соответственно 1, 2, 3, …, т.е.
имеют столько положительных
единиц, сколько нулей стоит в
логарифмируемом числе после единицы. Логарифмы чисел 0.1, 0.01, 0.001, ...
pавны
соответственно –1,
–2,
–3, …, т.е. имеют столько
отрицательных единиц, сколько нулей стоит в логарифмируемом числе перед единицей
(
считая и нуль целых
). Логарифмы
остальных чисел имеют дробную
часть, называемую мантиссой. Целая
часть логарифма называется
характеристикой. Для практического применения
десятичные логарифмы наиболее удобны.
Натуральным
логарифмом
называется логарифм по основанию
е.
Он обозначается
ln
, т.е. log
e
N
= ln
N.
Число е
является иррациональным, его
приближённое
значение 2.718281828.
Оно
является пределом,
к которому стремится число (
1 + 1
/
n )
n
при
неограниченном возрастании
n
( см. так называемый второй замечательный предел в разделе
"Пределы"
). Как это ни покажется
странным, натуральные логарифмы оказались очень удобными при
проведении различного рода операций,
связанных с анализом функций.
Вычисление
логарифмов по основанию
е
осуществляется
гораздо
быстрее,
чем по любому другому основанию.
| 


