Свойства корней квадратного уравнения. Теорема Виета

Свойства корней квадратного уравнения.

Дискриминант. Теорема Виета.

    Формула корней неприведенного квадратного уравнения:

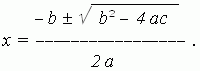
показывает, что возможны три случая:

           1)  b ² – 4 a c > 0 ,  тогда имеются два различных корня;

           2)  b ² – 4 a c = 0 ,  тогда имеются два равных корня;

           3)  b ² – 4 a c < 0 ,  тогда имеются два комплексных корня.

Выражение  b ² – 4 a c, от значения которого зависит, какой случай имеет место, называется дискриминантом квадратного уравнения и обозначается через D.

Теорема Виета. Сумма корней приведенного квадратного уравнения x² + px+ q = 0 равна коэффициенту при первой степени неизвестного, взятому с обратным знаком: 

x₁ +  x₂ = – p ,

а произведение равно свободному члену:

x₁ ·  x₂ =  q .

Для доказательства теоремы Виета достаточно воспользоваться формулой корней приведенного квадратного уравнения.